Noi deriviamo la composizione relativistica delle velocità dai principi di conservazione dell’energia e della quantità di moto, senza l’utilizzo della trasformazione di Lorentz.
Dopo le dimostrazioni del principio di equivalenza fra energia e massa E=mc², della formula della massa e dell’energia relativistica, la seguente derivazione della composizione relativistica delle velocità rappresenta il quarto anello nella catena di dimostrazioni che, partendo dalla fisica classica, conduce alla Teoria della Relatività Speciale su un percorso alternativo semplice e intuitivo.
Descrizione della dimostrazione in forma ridotta
(La dimostrazione dettagliata è descritta nel decimo capitolo del libro “Newton e la Relatività“).
Per la dimostrazione si considera una collisione centrale di due particelle che dia luogo alla formazione di una nuova particella.
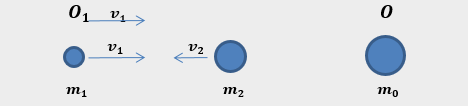
I due osservatori O e O1 in moto relativo fra di loro esaminano l’esperimento indipendentemente l’uno dall’altro (vedi l’animazione) applicando i principi di conservazione dell’energia e della quantità di moto.
L’osservatore O misura le velocità delle particelle
L’osservatore O, trovandosi in quiete con la particella formata, può misurare le velocità delle particelle collidenti.
Egli calcola l’energia del sistema in funzione di queste velocità con l’espressione:
\[ \frac{m_{01}c^2}{\sqrt{1-\frac{v_1^{2}}{c^{2}}}}+\frac{m_{02}c^2}{\sqrt{1-\frac{v_2^{2}}{c^{2}}}}=m_0c^2 \quad \]equiparando la somma delle energie delle particelle collidenti con l’energia della particella formatasi dopo la collisione.
L’osservatore O1 misura la velocità relativa fra le particelle
L’osservatore O1, trovandosi in quiete con una delle due particelle collidenti, può misurare la velocità dell’altra particella collidente. Questa corrisponde alla velocità relativa fra le due particelle.
O1 esegue il calcolo della quantità di moto del sistema prima e dopo l’urto in funzione della velocità relativa v12 e della velocità v1 della particella formatasi in seguito della collisione:
\[ \frac{m_{02}v_{12}}{\sqrt{1-\frac{v_{12}^{2}}{c^{2}}}}=\frac{m_{0}v_{1}}{\sqrt{1-\frac{v_1^{2}}{c^{2}}}} \]La velocità relativa è la somma relativistica delle velocità
La velocità relativa v12 fra le due particelle, misurata dall’osservatore O1, rappresenta la somma relativistica delle velocità delle singole particelle.
Per completare la dimostrazione si imposta un’equazione usando i risultati dei due osservatori.
In questo modo si ottiene l’espressione finale della velocità relativa in funzione delle velocità delle singole particelle:
\[ v_{12} = \frac{v_1 + v_2}{1 + \frac{v_1v_2}{c^2}} \]Quest’espressione rappresenta la composizione relativistica delle velocità.
La dimostrazione dettagliata della composizione relativistica delle velocità è riportata nel decimo capitolo del libro “Newton e la Relatività“.
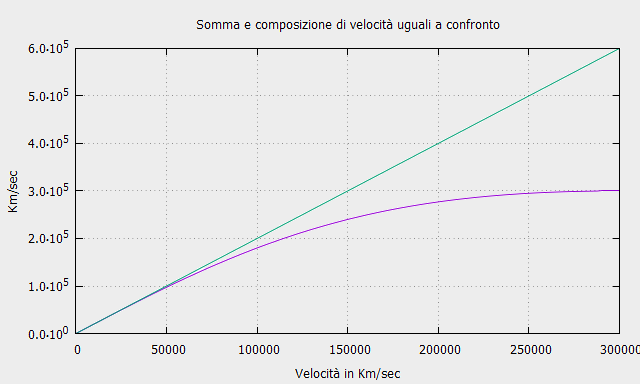
Un’altra dimostrazione più semplice è valida per la composizione relativistica di velocità uguali.
Con il Relativistic Calculator puoi calcolare l’addizione relativistica di due velocità.
Prosegui sul percorso alternativo delle dimostrazioni relativistiche: dimostrazione della costanza della velocità della luce.
Leave a Reply