Una derivazione alternativa della massa relativistica può essere effettuata partendo dalla Seconda Legge della Dinamica di Newton in connessione col principio di equivalenza E=mc² fra energia e massa.
Spiegazione euristica della dipendenza della massa dalla velocità
Prima di farne la dimostrazione vogliamo offrire una spiegazione concettuale della dipendenza della massa dalla velocità.
Gli esperimenti negli acceleratori di particelle manifestano un fenomeno apparentemente inspiegabile con la Meccanica newtoniana:
L’inerzia delle particelle aumenta all’aumentare della loro velocità.
In quest’articolo vedremo che questo fenomeno è una conseguenza del principio di equivalenza (E=mc²) fra massa ed energia. Quest’ultimo è derivabile con le leggi della fisica classica (vedi qui).
Con la dimostrazione del principio di equivalenza abbiamo mostrato che l’assorbimento di energia radiante da parte di un corpo materiale è accompagnato da un aumento della massa del corpo stesso.
Supposto che E sia l’energia assorbita, l’incremento di massa è uguale al quoziente E/c².
Basandoci sul principio di conservazione è logico estendere questa proprietà anche a tutte le altre forme di energia come segue:
Un assorbimento di energia determina un aumento di massa di un sistema fisico secondo l’equivalenza massa-energia E=mc².
Questo è anche ciò che si verifica quando un corpo materiale non vincolato è sottoposto a una forza esterna.
Infatti in questo caso si ha un’accelerazione accompagnata da un aumento di energia cinetica e, conseguentemente, di massa.
Schematicamente:
Aumento di velocità –> Aumento di energia cinetica –> Aumento di massa
In termini quantitativi questo concetto si traduce nella seguente identità:
Massa del corpo in moto = massa del corpo in quiete + massa dell’energia cinetica del corpo.
Di conseguenza:
La massa di un corpo dipende dalla sua energia cinetica
Perciò un aumento di velocità causa un incremento della massa del “sistema” composto dal corpo materiale e dalla sua energia.
La dipendenza della massa dalla velocità è quindi una diretta conseguenza del principio di equivalenza fra massa ed energia.
Con questo concetto divergiamo in questo sito dalle dimostrazioni convenzionali della formula di massa relativistica.
L’interpretazione di Lorentz e Einstein si basa infatti sulla contrazione delle lunghezze ed è perciò difficile da recepire.
Un aumento di massa dovuto all’incremento dell’energia cinetica è invece intuitivamente chiaro.
Premesso questo, possiamo ora procedere con la derivazione della formula di massa relativistica.
Dopo quella di E=mc² con la fisica classica, questa è la seconda dimostrazione di fondamentale importanza per i fini di questo sito web.
Infatti, con la seguente derivazione della massa relativistica si ottiene la prima relazione contenente il fattore di Lorentz.
Si entra quindi nel campo di applicazione della Teoria della Relatività partendo dalla Meccanica newtoniana, senza presupporre né il postulato della costanza della velocità della luce, né l’utilizzo delle trasformazioni di Lorentz.
D’altra parte, la formula della massa relativistica rappresenta la relazione basilare nel percorso alternativo qui trattato.
Infatti, essa viene utilizzata per ricavare tutte le altre dimostrazioni ivi compresa quella teorica della costanza della velocità della luce.
Descrizione della dimostrazione in forma ridotta
(Per la versione dettagliata della dimostrazione rimandiamo al quinto capitolo del libro “Newton e la Relatività”).
Se il percorso infinitesimale ds procede nella stessa direzione di una forza F agente su un corpo, allora dalla relazione della Seconda Legge della Dinamica …
\[ \vec{F} = \frac{d(m\vec{v})}{dt} = m\frac{d\vec{v}}{dt} + \vec{v}\frac{dm}{dt} \]… può essere derivata direttamente la seguente equazione differenziale per il lavoro e l’energia:
\[ Fds = dE = mvdv + v^2dm\]Si noti che il termine v²dm consente l’ipotesi di una massa variabile, come effettivamente avviene alle alte velocità.
Se si sostituisce il termine equivalente della massa c²dm all’energia cinetica arrecata dE e si integra l’equazione differenziale risultante …
\[c^2dm = mvdv + v^2dm\] \[\frac{dm}{m} = \frac{v}{c^2-v^2}dv\] \[\int_{m_{0}}^m\frac{dm}{m} = \int_0^v\frac{v}{c^2-v^2}dv\] \[[ln(m)]_{m_{0}}^m=-\frac{1}{2}[ln(c^2-v^2)]_0^v\] \[ln\frac{m}{m_0}=\frac{1}{2}ln\frac{c^2}{c^2-v^2}\] \[\frac{m}{m_0}=\sqrt{\frac{c^2}{c^2-v^2}}\]… si ottiene la formula della massa relativistica:
\[ m = \frac{m_{0}}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \]dove:
\[ \frac{1}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \]è il fattore di Lorentz.
Il procedimento adottato per dimostrare la formula della massa relativistica fornisce un primo indizio rivelatore della compatibilità del Secondo Principio della Dinamica di Newton con la Relatività.
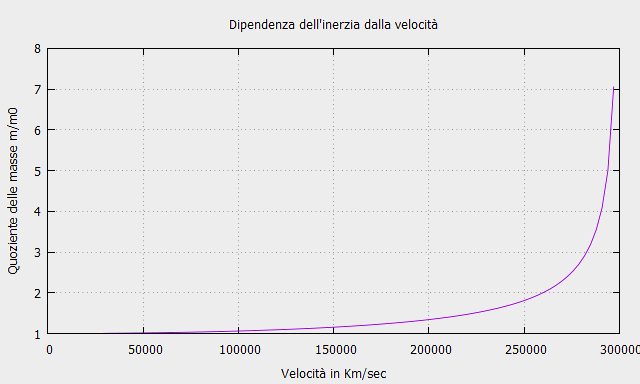
Il conseguente uso di massa variabile nella legge di Newton mostra che la Teoria della Relatività Ristretta può essere raggiunta con una logica estensione della meccanica classica.
L’applicazione dei principi di conservazione dell’energia e della quantità di moto, con l’utilizzo della massa relativistica, consente la derivazione alternativa delle relazioni della Teoria della Relatività Speciale (a questo riguardo vedi la pagina: “Sequenza di dimostrazioni relativistiche“).
La versione dettagliata di questa derivazione della massa relativistica è riportata nel quinto capitolo del libro “Newton e la Relatività“.
______________
Con il Relativistic Calculator puoi calcolare il fattore di Lorentz in funzione della velocità.
Prosegui sul percorso alternativo delle dimostrazioni relativistiche: derivazione dell’energia relativistica.
Leave a Reply