Herleitung der relativistischen Massenformel

Eine alternative Herleitung der relativistischen Massenformel kann ausgehend von Newtons zweitem Gesetz der Dynamik in Verbindung mit dem Äquivalenzprinzip von Energie und Masse E=mc² erfolgen.

Heuristische Erklärung der Massenabhängigkeit von der Geschwindigkeit

Bevor wir die Abhängigkeit der Masse von der Geschwindigkeit beweisen, wollen wir zuerst eine schlüssige Erklärung davon geben.

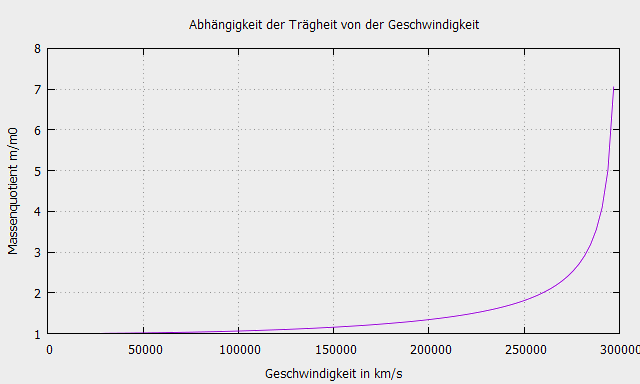
Experimente in Teilchenbeschleunigern zeigen ein mit der Newtonschen Mechanik scheinbar unerklärliches Phänomen:

Die Trägheit der Teilchen nimmt mit zunehmender Geschwindigkeit zu.

In diesem Artikel werden wir sehen, dass dieses Phänomen eine Folge des Äquivalenzprinzips (E=mc²) zwischen Masse und Energie ist. Letzteres lässt sich aus den Gesetzen der klassischen Physik ableiten (siehe hier).

Mit der Herleitung des Äquivalenzprinzips haben wir gezeigt, dass mit der Absorption von Strahlungsenergie durch einen physikalischen Körper eine Zunahme der Masse des Körpers selbst einhergeht.

Angenommen, E ist die absorbierte Energie, dann ist die Massenzunahme gleich dem Quotienten E / c².

Unter Berücksichtigung des Energieerhaltungssatzes, lässt sich diese Eigenschaft auch auf alle anderen Energieformen, wie folgt, ausweiten:

Eine Energieaufnahme bewirkt eine Massenzunahme eines physikalischen Systems nach dem Masse-Energie-Äquivalenz E = mc².

Letzteres geschieht auch, wenn eine äußere Kraft auf einen ungebundenen Körper einwirkt.

Denn in diesem Fall findet eine Beschleunigung statt, mit einer Zunahme der kinetischen Energie und demzufolge der Masse.

Quantitativ lässt sich dieses Konzept in folgende Identität umsetzen:

Masse des bewegten Körpers = Masse des Körpers in Ruhezustand + Masse der kinetischen Energie des Körpers.

Konsequenterweise:

Die Trägheit eines Körpers hängt von seiner Bewegungsenergie ab

Eine Zunahme der Geschwindigkeit bewirkt folglich eine Zunahme der Masse des “Systems”, das aus dem Körper und seiner Energie besteht.

Die Abhängigkeit der Masse von der Geschwindigkeit ist also eine direkte Folge des Äquivalenzprinzips zwischen Masse und Energie.

Mit diesem Konzept weichen wir auf dieser Website von der etablierten Herleitung der relativistischen Massenformel ab.

Denn die Interpretation von Lorentz und Einstein basiert nämlich auf der Längenkontraktion und ist daher m. E. schwer begreiflich.

Stattdessen ist eine Massenzunahme wegen einer Erhöhung der kinetischen Energie leicht nachvollziehbar.

Dadurch wird außerdem eine direkte Verbindung zwischen newtonscher und relativistischer Mechanik erstellt.

Dies vorausgesetzt, können wir nun mit der Herleitung der relativistischen Massenformel fortfahren.

Nach der Herleitung von E=mc² mit der klassischen Physik ist dies der zweite Beweis von grundlegender Bedeutung für die Zwecke dieser Website.

In der Tat erhalten wir mit der folgenden Herleitung der relativistischen Massenformel die erste physikalische Beziehung, die den Lorentz-Faktor enthält.

Wir betreten daher das Anwendungsgebiet der Relativitätstheorie ausgehend von der Newtonschen Mechanik, ohne das Postulat der Konstanz der Lichtgeschwindigkeit vorauszusetzen und ohne die Verwendung der Lorentz-Transformationen vorzunehmen.

Andererseits stellt die relativistische Massenformel die grundlegende Beziehung in dem hier behandelten alternativen Weg dar.

Denn die Massenformel wird verwendet, um alle anderen physikalischen Beweise zu führen, einschließlich des theoretischen Beweises der Konstanz der Lichtgeschwindigkeit.

Kurzfassung der Herleitung der relativistischen Massenformel

(Für die detaillierte Version der Herleitung verweisen wir auf das fünfte Kapitel des Buches “Newton und die Relativität“).

Wenn der Weg ds in die gleiche Richtung der auf einen Körper einwirkenden Kraft F verläuft, dann lässt sich aus der Relation des Zweiten Gesetzes der Dynamik¹ …

\[ \vec{F} = \frac{d(m\vec{v})}{dt} = m\frac{d\vec{v}}{dt} + \vec{v}\frac{dm}{dt} \]

… folgende Differentialgleichung der Arbeit bzw. der Energie direkt ableiten:

\[ Fds = dE = mvdv + v^2dm\]

Es ist zu beachten, dass der Term v²dm die Hypothese einer variablen Masse zulässt, wie sie tatsächlich bei hohen Geschwindigkeiten auftritt.

Setzt man anstelle der zugefügten kinetischen Energie dE den äquivalenten Term der Masse c²dm und integriert die resultierende Differentialgleichung …

\[c^2dm = mvdv + v^2dm\] \[\frac{dm}{m} = \frac{v}{c^2-v^2}dv\] \[\int_{m_{0}}^m\frac{dm}{m} = \int_0^v\frac{v}{c^2-v^2}dv\] \[[ln(m)]_{m_{0}}^m=-\frac{1}{2}[ln(c^2-v^2)]_0^v\] \[ln\frac{m}{m_0}=\frac{1}{2}ln\frac{c^2}{c^2-v^2}\] \[\frac{m}{m_0}=\sqrt{\frac{c^2}{c^2-v^2}}\]

… dann erhält man die relativistische Massenformel:

\[ m = \frac{m_{0}}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \]

wobei:

\[ \frac{1}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \]

ist der Lorentz-Faktor.

Das Verfahren zum Nachweis der relativistischen Massenformel liefert einen aufschlussreichen Hinweis auf die Kompatibilität von Newtons Zweitem Prinzip der Dynamik mit der Relativitätstheorie.

Die konsequente Verwendung variabler Masse im Newtonschen Gesetz zeigt, dass die SRT als logische Erweiterung der klassischen Mechanik aufgefasst werden kann.

Die Anwendung der Energie- und Impulserhaltungssätze unter Verwendung der relativistischen Masse ermöglicht die alternative Herleitung der Formeln der Speziellen Relativitätstheorie (siehe hierzu die Seite: “Abfolge der relativistischen Herleitungen“).

Diese alternative Herleitung der relativistischen Massenformel wird in detaillierter Form im fünften Kapitel des Buches „Newton und die Relativität“ beschrieben.

Mit dem Relativistic Calculator können Sie den Lorentz-Faktor in Abhängigkeit von der Geschwindigkeit berechnen.

Weiter auf dem alternativen Weg der relativistischen Beweise: Alternative Herleitung der relativistischen Energie.

Zur Homepage

______________

Das Ziel dieser Webseite ist es, die Relativitätstheorie mit einer neuen, einfachen und zugänglichen Demonstrationsmethode zu ergründen.

Um dieses Projekt zu unterstützen, bestellen Sie bitte das Buch “Newton und die Relativität“.

______________

Fußnoten:

1. Newtons Zweites Gesetz der Dynamik wird konsequent, in seiner ursprünglichen Form verwendet, wonach die Kraft gleich der zeitlichen Ableitung des Impulses ist. Nach der Produktregel ergibt sich die Summe von zwei Termen. Bei niedrigen Geschwindigkeiten kann die Masse als konstant angesehen werden, so dass der zweite Term gleich Null gesetzt werden kann. Bei hohen Geschwindigkeiten muss dieser Term stattdessen auf der Grundlage der Abhängigkeit der Masse von der Geschwindigkeit berechnet werden. ↩︎