An alternative derivation of the relativistic mass formula can be made using Newton‘s Second Law of Motion in connection with the mass-energy equivalence principle E=mc².
Heuristic explanation of the mass dependence on velocity
Before proving the dependence of mass on velocity, we want to give a coherent explanation of it.
Experiments in particle accelerators show a phenomenon that seems inexplicable with Newtonian mechanics:
The inertia of the particles increases with increasing speed.
In this article we will see that this phenomenon is a consequence of the principle of equivalence (E=mc²) between mass and energy. The latter can be derived from the laws of classical physics (see here).
With the derivation of the equivalence principle, we have shown that the absorption of radiant energy by a physical body is accompanied by an increase in the mass of the body itself.
Assuming that E is the energy absorbed, the increase in mass is equal to the quotient E / c².
Considering the law of energy conservation, one can extend this property to all other energy forms as follows:
An energy absorption causes a mass increase of a physical system according to the mass-energy equivalence E = mc².
The latter also happens when an unbound body is subjected to an external force.
In fact, in this case, acceleration takes place, with a concomitant increase in kinetic energy and consequently in mass.
In quantitative terms, this concept translates into the following identity:
Mass of the moving body = mass of the body at rest + mass of the kinetic energy of the body.
Consequentially:
The inertia of a body depends on its kinetic energy
An increase in speed consequently causes an increase in the mass of the “system” composed of the body and its energy.
The dependence of mass on velocity is therefore a direct consequence of the principle of equivalence between mass and energy.
With this concept we deviate on this website from the established proofs of the relativistic mass formula.
The interpretation of Lorentz and Einstein is based on the length contraction and is therefore difficult to understand, in my opinion.
Instead, an increase in mass due to an increase in kinetic energy is easily plausible.
Having said that, we can now proceed with the derivation of the relativistic mass formula.
After E=mc² using classical physics, this is the second proof of fundamental importance for the purposes of this website.
In fact, with the following derivation of the relativistic mass formula, we get the first relation containing the Lorentz factor.
We therefore enter the field of application of the Theory of Relativity starting from Newtonian mechanics, without assuming either the postulate of the constancy of the speed of light nor using the Lorentz transformations.
On the other hand, the relativistic mass formula represents the basic relationship in the alternative path treated here.
The relativistic mass formula is indeed used to derive all the other proofs, including the theoretical one of the constancy of the speed of light.
Description of the proof in reduced form
(For the detailed version of the proof we refer to the fifth chapter of the book “Newton and Relativity“).
If the displacement ds runs in the same direction as the force F acting on a body, then from the relation of the Second Law of Motion …
\[ \vec{F} = \frac{d(m\vec{v})}{dt} = m\frac{d\vec{v}}{dt} + \vec{v}\frac{dm}{dt} \]… the following differential equation for work and energy can be derived directly:
\[ Fds = dE = mvdv + v^2dm\]Note that the term v²dm allows the hypothesis of a variable mass as it actually occurs at high speeds.
If, instead of the added kinetic energy dE the equivalent term of the mass c²dm is set and the resulting differential equation is integrated …
\[c^2dm = mvdv + v^2dm\] \[\frac{dm}{m} = \frac{v}{c^2-v^2}dv\] \[\int_{m_{0}}^m\frac{dm}{m} = \int_0^v\frac{v}{c^2-v^2}dv\] \[[ln(m)]_{m_{0}}^m=-\frac{1}{2}[ln(c^2-v^2)]_0^v\] \[ln\frac{m}{m_0}=\frac{1}{2}ln\frac{c^2}{c^2-v^2}\] \[\frac{m}{m_0}=\sqrt{\frac{c^2}{c^2-v^2}}\]… then you get the relativistic mass formula:
\[ m = \frac{m_{0}}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \]where:
\[ \frac{1}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \]is the Lorentz factor.
This shows the compatibility of Newton’s Second Law of Motion with Relativity.
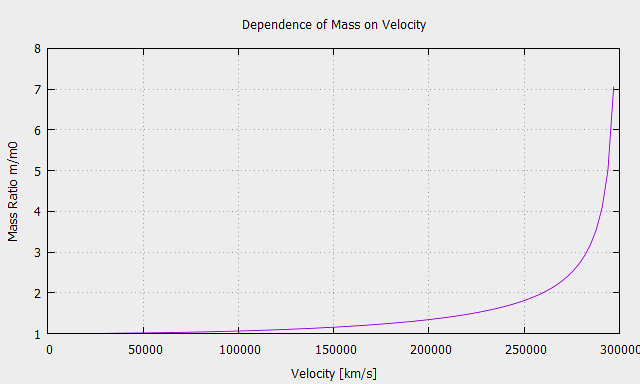
The consequent use of variable mass in Newton’s law shows that the Special Theory of Relativity can be reached by a logical extension of classical mechanics.
The application of the principles of conservation of energy and momentum using relativistic mass enables the alternative derivation of the relationships of Special Relativity (in this regard, see the page: “Sequence of Relativistic Proofs“).
The detailed version of this alternative derivation of the relativistic mass formula is given in the fifth chapter of the book “Newton and Relativity“.
______________
With the Relativistic Calculator you can calculate the Lorentz factor as a function of speed.
Continue on the alternative path of relativistic proofs: Alternative derivation of relativistic energy.
Leave a Reply