Der auf dieser Website beschriebene Beweis der Masse-Energie Äquivalenz E=mc² ist der erste Schritt auf einem alternativen Weg zur Relativitätstheorie.
Für den Nachweis der Äquivalenz von Masse und Energie ist die Relativitätstheorie nicht erforderlich.
In der Tat hat Einstein selbst gezeigt (siehe: Max Born – Die Relativitätstheorie Einsteins – S. 244-247), dass sich die Beziehung E=mc² auf sehr einfache Weise allein aus den Gesetzen der klassischen Physik ableiten lässt.
Im dritten und vierten Kapitel des Buches “Newton und die Relativität” wird gezeigt, dass die Äquivalenz von Masse und Energie eine Folge der Impulserhaltung bei der Wechselwirkung zwischen Materie und elektromagnetischer Strahlung ist.
Zu diesem Thema können Sie auch ein Video anschauen und ein Audio anhören.
Beweis der Masse-Energie Äquivalenz E=mc² basierend auf dem “Strahlungsdruck” von Francesco Cester
Die Herleitung beruht darauf, dass ein ruhender Körper, der Strahlung aussendet, einen Gegenimpuls erhält.
Demzufolge bewegt er sich in die entgegengesetzte Richtung der Strahlung.
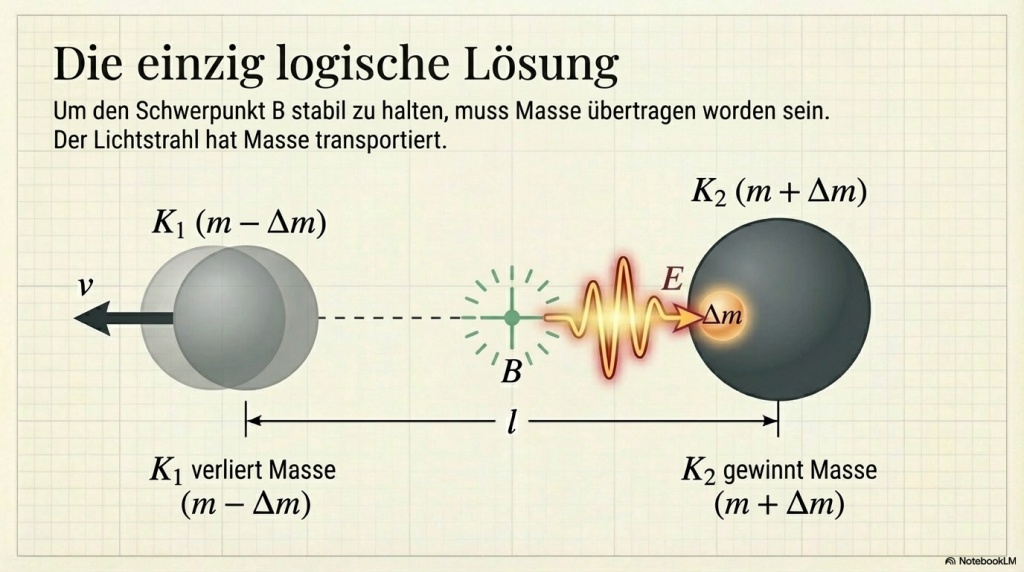
In einem isolierten physikalischen System betrachten wir die Emission und Absorption von Strahlung zwischen zwei identischen Körpern der Masse m:
Klicken Sie auf die rechteckige Fläche, um den Prozess zu veranschaulichen
Nach dem internen Energieaustausch bleibt der Massenschwerpunkt des physikalischen Systems in Ruhe.
Da sich der emittierende Körper nach dem Aussenden der Strahlung in einem größeren Abstand zum Massenschwerpunkt befindet als der absorbierende Körper, hat sich seine Masse folglich verringert.
Auf der Grundlage einer rein experimentellen Analyse lässt sich also Folgendes ableiten:
Ein Körper, der elektromagnetische Energie abstrahlt, verliert Masse.
Und folglich:
Ein Körper, der elektromagnetische Energie aufnimmt, gewinnt an Masse.
Aus rein theoretischer Sicht bedeutet dies:
Die Impulsbilanz zwischen Materie und Strahlung reicht aus, um den Massengewinn eines absorbierenden Körpers und den Massenverlust eines emittierenden Körpers zu berechnen.
Mit Hilfe eines Gedankenexperiments (siehe Animation) lässt sich die Gleichung E=mc² auf einfache Weise aus der Beziehung des elektromagnetischen Impulses p=E/c ableiten.
Beschreibung der Herleitung in gekürzter Fassung
(Für die detaillierte Version des Beweises verweisen wir auf das dritte Kapitel des Buches „Newton und die Relativität“).
Das oben erwähnte Gedankenexperiment erlaubt es, drei physikalische Aspekte zu berücksichtigen. Diese bieten die Möglichkeit, ebenso viele elementare Beziehungen aufzustellen.
- Die erste Beziehung betrifft die Zeiten:
In der Zeit Δt, die die Strahlung benötigt, um den absorbierenden Körper auf der rechten Seite zu erreichen, legt der emittierende Körper auf der linken Seite die Strecke Δl mit der Geschwindigkeit v zurück:
\[ \Delta t=\frac{l}{c}=\frac{\Delta l}{v} \]Dabei ist l der anfängliche Abstand zwischen den beiden Körpern und c die Lichtgeschwindigkeit.
- Die zweite Beziehung bezieht sich auf die Lage des Schwerpunkts, die - trotz der Verschiebung des emittierenden Körpers - unverändert bleibt:
Wobei Δm die vom emittierenden Körper abgegebene und vom absorbierenden Körper aufgenommene Masse darstellt.
- Die dritte und letzte Beziehung ergibt sich aus dem Impulserhaltungssatz.
Nach diesem Prinzip ist der Impuls der emittierten Strahlung E/c gleich dem Impuls des emittierenden Körpers:
\[ (m-\Delta m)v=\frac{E}{c} \]Wobei E die Energie der elektromagnetischen Strahlung ist.
Die Lösung des Gleichungssystems aus den drei obigen Relationen ergibt die Beziehung
\[ \Delta m=\frac{E}{c^2} \]des Äquivalenzprinzips zwischen Masse und Energie.
Beweis der Masse-Energie Äquivalenz E=mc² aus dem Doppler-Effekt
Eine weitere einfache Herleitung des Masse-Energie-Äquivalenzprinzips kann mit Hilfe des Dopplereffekts der elektromagnetischen Strahlung erfolgen.
Als Gedankenexperiment dient die Annihilation des Elektron-Positron-Paares.
Beschreibung der Herleitung in reduzierter Form
(Für die detaillierte Version der Herleitung verweisen wir auf das vierte Kapitel des Buches “Newton und die Relativität“).
Aus dem Zerfall des durch die Elektron-Positron-Kollision gebildeten Teilchens kann die Emission zweier Photonen in entgegengesetzte Richtungen erfolgen (siehe Animation).

Für einen Beobachter, der sich mit der Geschwindigkeit v (v << c) in Richtung eines der beiden Photonen bewegt, gilt aufgrund der Impulserhaltung vor und nach der Photonenbildung folgende Relation:
\[m_0v=\frac{hf}{c}(1+\frac{v}{c})-\frac{hf}{c}(1-\frac{v}{c})\quad\quad(1) \]Wobei:
m0 ist die Masse des nach der Annihilation gebildeten instabilen Teilchens
c ist die Lichtgeschwindigkeit im Vakuum
h ist das Plancksche Wirkungsquantum
f ist die zu den Photonen zugehörige elektromagnetische Frequenz
Da 2hf die Gesamtenergie E des Systems ist, ergibt sich aus der Beziehung (1):
E = m0c².
Der Nachweis von E=mc² aus der klassischen Physik stellt das Bindeglied zwischen Newtonscher und relativistischer Mechanik dar, wie die Herleitung der relativistischen Massenformel zeigt.
Weiter auf dem alternativen Weg der relativistischen Beweise: Alternative Herleitung der Massenformel.
______________
Das Ziel dieser Webseite ist es, die Relativitätstheorie mit einer neuen, einfachen und zugänglichen Demonstrationsmethode zu ergründen.
Um dieses Projekt zu unterstützen, bestellen Sie bitte das Buch “Newton und die Relativität“.



Etwas ist komisch bei dieser Herleitung.
Der Körper K1 verliert einen Teil seiner Masse. Nach der Herleitung wird diese Massenenergie integral in Strahlungsenergie E umgewandelt:
Massenenergie = E.
Wegen dem Rückstoss von K1 muss aber ein Teil der Massenenergie in kinetische Energie umgewandelt werden und es müsste gelten:
Massenenergie = E + Ekin.
Warum ist die kinetische Eergie in der Energiebilanz verschwunden?
Für diese Herleitung ist keine Energiebilanz erforderlich. Wenn wir dennoch eine aufstellen wollen, müssen wir berücksichtigen, dass Δm nicht die gesamte Masse ist, die sich in Energie umwandelt, sondern nur der Anteil, der sich in elektromagnetischer Strahlungsenergie umwandelt. Ein weiterer Massenanteil des Körpers K1 wandelt sich in seine kinetische Energie um.
Wenn Δm nicht die gesamte Masse ist, die sich in Energie umwandelt, dann taucht ein anderes Problem auf.
Nach der Herleitung ist der Impuls von K1 gleich (m – Δm) v. Die Geschwindigkeit v ist nicht relativistisch. Daher ist (m – Δm) auch die Masse, die in der kinetischen Energie vorkommt. Also muss Δm die gesamte Masse sein, welche in Energie umgewandelt wurde. Der Rest bleibt ja erhalten.
v ist doch eine relativistische Geschwindigkeit. Nach der Strahlungsemission stellt (m – Δm) nicht die Ruhemasse sondern die relativistische, geschwindigkeitsabhängige Masse des Körpers K1 mit seiner kinetischer Energie dar. Die Ruhemasse m0 von K1 lässt sich berechnen, indem (m – Δm) durch den Lorentzfaktor geteilt wird. Der in kinetische Energie von K1 umgewandelte Massenanteil ist somit (m – Δm) – m0. All dies muss bei dieser Herleitung aber nicht unbedingt erwähnt werden.
Im ausführlicheren Text steht :
Wir betrachten ein physikalisches System, bestehend aus zwei gleichen Körpern K1 und K2 der Masse m, die anfänglich in einem Abstand l voneinander ruhen.
Daher habe ich angenommen, dass m die Ruhemasse ist.
Über der Animation steht:
In einem isolierten physikalischen System betrachten wir die Emission und Absorption von Strahlung zwischen zwei identischen Körpern der Masse m.
Weil einer der Körper in Ruhe ist, liegt es auf der Hand m als Ruhemasse aufzufassen.
Vor der Emission stellt m tatsächlich die Ruhemasse von K1 dar.
Nach der Emission hat K1 jedoch Masse verloren, sodass seine Ruhemasse kleiner geworden ist.
Ein Teil der verlorenen Masse ist in die Energie der elektromagnetischen Strahlung und ein weiterer Teil in die kinetische Energie von K1 selbst übergegangen.
Übrigens, eine Antwort auf Ihren Kommentar auf der englischen Startseite wird noch demnächst folgen.
Vielen Dank für Ihr Interesse.
THEORIE UND POESIE
( Einstein relativ lyrisch )
Newtons Gesetze sind phänomenal,
Einstein modernisierte sie genial.
Am Anfang war der Urknall,
aus der Singularität;
das Duo Raum und Zeit entsteht,
das expandierende Weltall.
Von den Nukleonen, winzig klein,
bis zum größten Galaxienverein;
wie alles ablief, weiß Gott allein.
Ein Fall für Albert Einstein.😉
Weltbekannt sein Resultat:
E = m c ²
Er postulierte die Raumzeit,
den gekrümmten Raum als Neuheit.
Dunkle Materie ist rätselhaft,
dunkle Energie nicht minder.
Das Wissen ist noch lückenhaft,
man kommt nicht recht dahinter.
Es braucht wohl wieder ein Genie,
gar eine neue Theorie.
Des Universums Architektur –
Was ist der Sinn von allem nur?
Das Weltall in Expansion
Milliarden Jahre nun schon.
Es sind dabei die Galaxien
einander rasant zu entflieh’n.
Konstant bewegt sich das Licht,
schneller geht es nunmal nicht.
Über Photonen und Quanten
ist manches noch unverstanden.
Vieles wird man noch ergründen,
der Mensch wird suchen und finden.
Rainer Kirmse , Altenburg
Herzliche Grüße aus Thüringen
Einfach großartig. Herzlichen Dank!
Bei dem Beweis über den Dopplerefekt benutzen Sie aber das Ergebnis des Michelson -Experiments. Denn die angegebene Gleichung gilt nur, wenn es keinen Äther gibt. Und das wissen wir erst nach diesem Versuch, der ja die Relativitätstheorie begründete. Mit Äther ergibt sich mit der Gleichung keine Masse-Energie-Äquivalenz. Die anderen von Ihnen angeführten Beweise habe ich noch nicht genau geprüft.
Grüße
Gunter Berauer
Hallo Herr Berauer,
Es stimmt. Relation (1) ist ein Ergebnis des Michelson-Experiments. Der hier aufgeführte Beweis ist eine kurze Zusammenfassung einer ausführlicheren Herleitung. Diese Herleitung finden Sie im dritten Kapitel meines Buches „Newton und die Relativität”. In der Fußnote auf der vierten Seite des Kapitels wird ausführlich auf die Frage eingegangen, die Ihren Kommentar ausgelöst hat.
Francesco Cester