Wir leiten die relativistische Addition der Geschwindigkeiten aus den Energie- und Impulserhaltungssätzen ab, ohne die Verwendung der Lorentz-Transformation.
Nach den Herleitungen des Äquivalenzprinzips von Energie und Masse E = mc², der relativistischen Massenformel und der relativistischen Energie stellt folgender Beweis der relativistischen Geschwindigkeitsaddition das vierte Glied in der Beweiskette dar, die, ausgehend von der klassischen Physik, auf einem einfachen und intuitiven Alternativweg zur Speziellen Relativitätstheorie führt.
Beschreibung des Beweises in reduzierter Form
(Für die detaillierte Version der Herleitung verweisen wir auf das zehnte Kapitel des Buches “Newton und die Relativität“).
Für die Herleitung betrachten wir eine zentrale Kollision zweier Teilchen, die zur Bildung eines neuen Teilchens führt.
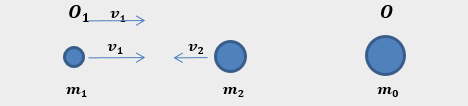
Die beiden Beobachter O und O1 in Relativbewegung zueinander untersuchen das Experiment (siehe die Animation) unabhängig voneinander, unter Verwendung der Energie- und Impulserhaltungsätze.
Beobachter O misst die Geschwindigkeiten der Teilchen
Beobachter O, der sich in Ruhezustand zum gebildeten Teilchen befindet, kann die Geschwindigkeiten der kollidierenden Teilchen messen.
Er berechnet die Energie des Systems in Abhängigkeit von diesen Geschwindigkeiten mit dem Ausdruck:
\[ \frac{m_{01}c^2}{\sqrt{1-\frac{v_1^{2}}{c^{2}}}}+\frac{m_{02}c^2}{\sqrt{1-\frac{v_2^{2}}{c^{2}}}}=m_0c^2 \quad \]durch Gleichsetzen der Summe der Energien der kollidierenden Teilchen mit der Energie des nach der Kollision gebildeten Teilchens.
Beobachter O1 misst die relative Geschwindigkeit zwischen den Teilchen
Beobachter O1, der mit einem der beiden kollidierenden Teilchen in Ruhe ist, kann die Geschwindigkeit des anderen Teilchens messen, die der Relativgeschwindigkeit zwischen den Teilchen entspricht.
O1 berechnet den Impuls des Systems vor und nach der Kollision in Abhängigkeit von der Relativgeschwindigkeit v12 und der Geschwindigkeit v1 des nach der Kollision gebildeten Teilchens:
\[ \frac{m_{02}v_{12}}{\sqrt{1-\frac{v_{12}^{2}}{c^{2}}}}=\frac{m_{0}v_{1}}{\sqrt{1-\frac{v_1^{2}}{c^{2}}}} \]Die Relativgeschwindigkeit ist die relativistische Summe der Geschwindigkeiten
Die von Beobachter O1 gemessene Relativgeschwindigkeit v12 zwischen den beiden Teilchen stellt die relativistische Summe der Geschwindigkeiten der einzelnen Teilchen dar.
Um den Beweis fertigzustellen, wird eine Gleichung unter Verwendung der Ergebnisse der beiden Beobachter aufgestellt.
Auf diese Weise wird der endgültige Ausdruck der Relativgeschwindigkeit in Abhängigkeit von den Geschwindigkeiten der einzelnen Teilchen erhalten:
\[ v_{12} = \frac{v_1 + v_2}{1 + \frac{v_1v_2}{c^2}} \]Diese Relation stellt die relativistische Addition der Geschwindigkeiten dar.
Die detaillierte Version des Beweises der relativistischen Addition der Geschwindigkeiten wird im zehnten Kapitel des Buches „Newton und die Relativität“ beschrieben.
Ein weiterer einfacherer Beweis gilt für die relativistische Addition gleicher Geschwindigkeiten.
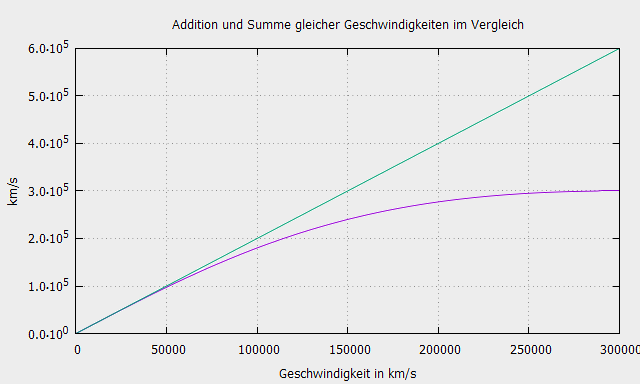
Mit dem Relativistic Calculator können Sie die relativistische Addition der Geschwindigkeiten berechnen.
Weiter auf dem alternativen Weg der relativistischen Beweise: Beweis der Konstanz der Lichtgeschwindigkeit.
Leave a Reply