Herleitung der relativistischen Energie

Die Herleitung der relativistischen Energie kann direkt aus der Äquivalenz von Masse und Energie unter Anwendung der relativistischen Massenformel erfolgen.

Heuristische Erklärung der Herleitung

Aus dem Masse-Energie-Äquivalenzprinzip folgt, dass die Energie, die einer Masse m₀ entspricht, gleich m₀c² ist.

Beim Beweis des obigen Prinzips (siehe hier) wurde angenommen, dass sich die Masse m₀ in Ruhezustand befindet.

Diese Voraussetzung ist jedoch nicht erforderlich. Das bedeutet, dass die Äquivalenz von Masse und Energie auch auf bewegte Massen ausgeweitet werden kann.

Im allgemeinsten Fall kann das Äquivalenzprinzip durch die folgende Beziehung ausgedrückt werden:

\[E=\frac{m_0c^2}{\sqrt{1-\frac{v^{2}}{c^{2}}}}\quad\quad (1)\]

die man erhält, wenn man die ruhende Masse durch den entsprechenden Term einer bewegten Masse in Abhängigkeit von der Geschwindigkeit ersetzt.

Im letzteren Fall drückt die Beziehung (1) die Gesamtenergie eines bewegten physikalischen Körpers aus.

Da es sich um einen ungebundenen Körper handelt, ist seine Gesamtenergie notwendigerweise nur gleich der Summe seiner kinetischen Energie und seiner Ruheenergie:

\[\frac{m_0c^2}{\sqrt{1-\frac{v^{2}}{c^{2}}}}=E_c+m_0c^2\]

Für die kinetische Energie gilt dann:

\[E_c=\frac{m_0c^2}{\sqrt{1-\frac{v^{2}}{c^{2}}}}-m_0c^2\]

Bis zu diesem Punkt haben wir eine Ableitung der relativistischen Energie in Verbindung mit einer heuristischen Erklärung gegeben.

Nun wollen wir sehen, wie durch die Verwendung des zweiten Newtonschen Gesetzes der Dynamik eine rigorose Herleitung derselben Beziehung zwischen der kinetischen Energie und der Gesamtenergie des physikalischen Körpers erfolgen kann.

Herleitung der relativistischen Energie mit dem Newtonschen Gesetz

Das zweite Gesetz der Dynamik erlaubt in Verbindung mit E=mc² und mit der relativistischen Massenformel eine alternative Herleitung der relativistischen Energie des physikalischen Körpers.

Sowohl das Äquivalenzprinzip von Energie und Masse E=mc² als auch die Formel der Masse als Funktion der Geschwindigkeit wurden ohne Zuhilfenahme relativistischer Axiome bewiesen. Diese Herleitung der relativistischen Energie stellt somit das dritte Glied in der Beweiskette dar, die, ausgehend von der klassischen Physik, auf einem einfachen und nachvollziehbaren Alternativweg zur Speziellen Relativitätstheorie führt.

Die hier abgeleitete Formel der relativistischen Energie wird später zusammen mit der des Impulses verwendet, um alle anderen Formeln der Speziellen Relativitätstheorie zu beweisen, einschließlich der Beziehung der relativistischen Geschwindigkeitsaddition.

Letztere Beziehung ermöglicht somit den theoretischen Nachweis der Konstanz der Lichtgeschwindigkeit zu erbringen.

Beschreibung des Beweises in reduzierter Form

(Für die detaillierte Version der Herleitung klicken Sie hier).

Für den allgemeineren Fall mit veränderlichen Massen bei hohen Geschwindigkeiten wird die folgende Differentialgleichung aus dem Gesetz Newtons abgeleitet:

\[ dE_k = v^2dm+mvdv \quad\quad (1.5) \]

Die Beziehung (1.5) gilt für die infinitesimale Veränderung der kinetischen Energie eines ungebundenen Körpers, der einer konstanten Kraft in die Bewegungsrichtung ausgesetzt ist.

Wenn in der Beziehung (1.5) dm und m durch die Beziehungen des Masse-Energie-Äquivalenzprinzips (6.2) und der relativistischen Masse (5.4) ersetzt werden, …

\[ dm = \frac{dE_k}{c^2} \quad \quad \quad\quad(6.2)\] \[ m = \frac{m_0}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \quad\quad\quad(5.4)\]

.. erhält man die folgende Differentialgleichung:

\[ dE_k =v^2\frac{dE_k}{c^2}+\frac{m_0}{\sqrt{1-\frac{v^{2}}{c^{2}}}}vdv \quad \]

deren Integration den Ausdruck der relativistischen kinetischen Energie liefert:

\[ E_k = \frac{m_0c^2}{\sqrt{1-\frac{v^{2}}{c^{2}}}} – m_0c^2\quad\quad (6.4) \]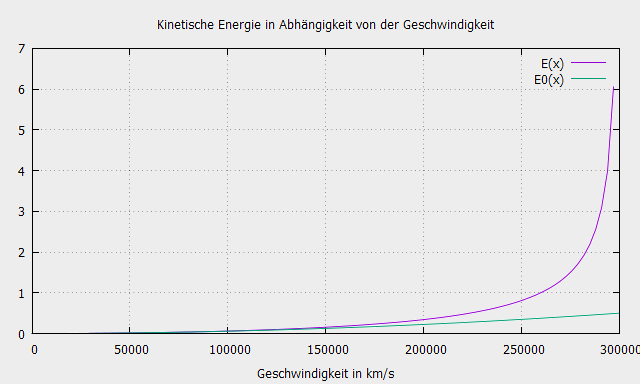

Da m₀c² der Energie der ruhenden Masse entspricht, folgt aus (6.4), dass die Relation:

\[ \frac{m_0c^2}{\sqrt{1-\frac{v^{2}}{c^{2}}}} = mc^2 \quad \]

die Gesamtenergie darstellt, die gleich der Summe der Ruheenergie und der kinetischen Energie des ungebundenen Körpers ist.

Diese Herleitung zeigt einen weiteren Fall von Kompatibilität des Newtonschen Gesetzes mit der Relativitätstheorie.

Diese alternative Herleitung der relativistischen Energie wird im sechsten Kapitel des Buches „Newton und die Relativität“ ausführlich beschrieben.

Mit dem Relativistic Energy Calculator können Sie die Energie eines Körpers in Abhängigkeit von seiner Masse und Geschwindigkeit berechnen.

Weiter auf dem alternativen Weg der relativistischen Beweise:

Lesen Sie, wie sich unter Verwendung der hier hergeleiteten Gesamtenergie die relativistische Addition der Geschwindigkeiten ableiten lässt.

Zur Homepage

______________

Das Ziel dieser Webseite ist es, die Relativitätstheorie mit einer neuen, einfachen und zugänglichen Demonstrationsmethode zu ergründen.

Um dieses Projekt zu unterstützen, bestellen Sie bitte das Buch “Newton und die Relativität“.