The derivation of relativistic energy follows directly from the mass-energy equivalence applied to the relativistic mass formula.
Heuristic explanation of the derivation
It follows from the energy-mass equivalence principle that the energy corresponding to a mass m0 is equal to m0c2.
In the derivation of the above principle (see here) it was assumed that the mass m0 is at rest.
However, this condition is not necessary. Therefore, this implies the possibility of extending energy-mass equivalence to masses in motion as well.
In the most general case, the equivalence principle can be expressed by the following relationship:
\[E=\frac{m_0c^2}{\sqrt{1-\frac{v^{2}}{c^{2}}}}\quad\quad (1)\]obtained by substituting for the mass at rest the corresponding term for a mass in motion in dependence on velocity.
In the latter case, relation (1) expresses the total energy of a material body in motion.
Since it is an unconstrained body, its total energy must necessarily be equal only to the sum of its kinetic and rest energy:
\[\frac{m_0c^2}{\sqrt{1-\frac{v^{2}}{c^{2}}}}=E_k+m_0c^2\]As a result, the following relationship applies to kinetic energy:
\[E_k=\frac{m_0c^2}{\sqrt{1-\frac{v^{2}}{c^{2}}}}-m_0c^2\]So far, we have provided a derivation of relativistic energy in conjunction with a heuristic explanation of it.
Now let us see how Newton’s Second Law of Motion can provide a rigorous derivation of the same relation of kinetic and total energy of the material body.
Derivation with Newton’s law
Newton‘s Second Law of Motion in connection with E=mc² and with the relativistic mass formula provides an alternative derivation of the relativistic energy of the physical body.
Since both the equivalence principle of mass and energy E=mc² and the formula of mass as a function of velocity have been proved without the aid of relativistic axioms, this derivation of relativistic energy represents the third link in the chain of proofs which, starting from classical physics, leads to the Theory of Special Relativity on a simple and intuitive path.
The relativistic energy formula obtained here is used later, together with that of momentum, to demonstrate all the other formulas of Special Relativity, including that of the relativistic addition of velocities.
This last relationship therefore allows the theoretical proof of the constancy of the speed of light.
Description of the proof in reduced form
(For the detailed version, click here).
In the more general case, which also provides for variable masses at high speeds, Newton’s Second Law yields the following differential equation (see here):
\[ dE_k = v^2dm+mvdv \quad\quad (1.5) \]The relation (1.5) is valid for the infinitesimal increase in the kinetic energy of an unconstrained physical body subject to a constant force in the same direction of motion.
From relation (1.5) by replacing dm and m with the relations of mass-energy equivalence principle (6.2) and relativistic mass (5.4):
\[ dm = \frac{dE_k}{c^2} \quad \quad \quad\quad(6.2)\] \[ m = \frac{m_0}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \quad\quad\quad(5.4)\]We obtain the following differential equation:
\[ dE_k =v^2\frac{dE_k}{c^2}+\frac{m_0}{\sqrt{1-\frac{v^{2}}{c^{2}}}}vdv \quad \]whose integration provides the expression of relativistic kinetic energy:
\[ E_k = \frac{m_0c^2}{\sqrt{1-\frac{v^{2}}{c^{2}}}} – m_0c^2\quad\quad (6.4) \]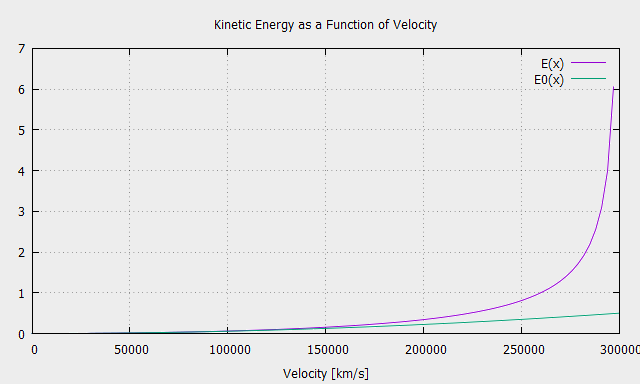
Since m0c2 corresponds to the energy of the rest mass, from (6.4) it follows that the term:
\[ \frac{m_0c^2}{\sqrt{1-\frac{v^{2}}{c^{2}}}} = mc^2 \quad \]is the total energy, equal to the sum of the energy at rest and kinetic of the unconstrained body.
This derivation demonstrates a further case of compatibility of Newton’s law with the Theory of Relativity.
The detailed version of this derivation of relativistic energy occurs in the sixth chapter of the book “Newton and Relativity“.
To support this project, please order the book “Newton and Relativity“.
______________
With the Relativistic Energy Calculator you can calculate the energy of a physical body depending on its mass and speed.
Continue on the alternative path of relativistic proofs: Alternative proof of the addition of velocities.



Leave a Reply