We derive the relativistic addition of velocities from the laws of conservation of energy and momentum, without the Lorentz transformation.
After the derivations of the mass-energy equivalence principle E = mc², the relativistic mass formula and the relativistic energy, the following derivation of the relativistic addition of velocities is the fourth link in the chain of proofs that leads from classical physics to Special Relativity via a simple and intuitive alternative path.
Description of the proof in reduced form
(For the detailed version of the derivation, please refer to the tenth chapter of the book “Newton and Relativity”).
For the derivation, we consider a central collision of two particles, resulting in the creation of a new particle.
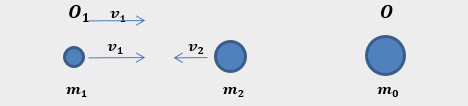
The two observers, O and O1, moving relative to each other, examine the experiment independently (see the animation), applying the principles of conservation of energy and momentum.
Observer O measures the speed of the particles
Observer O, who is at rest with the particle formed, can measure the velocities of the colliding particles.
He calculates the energy of the system as a function of these velocities using the expression:
\[ \frac{m_{01}c^2}{\sqrt{1-\frac{v_1^{2}}{c^{2}}}}+\frac{m_{02}c^2}{\sqrt{1-\frac{v_2^{2}}{c^{2}}}}=m_0c^2 \quad \]by equating the sum of the energies of the colliding particles with the energy of the particle formed after the collision.
Observer O1 measures the relative velocity between the particles
Observer O1, being at rest with one of the colliding particles, can measure the speed of the other particle. This is the relative velocity between the two particles.
O1 calculates the momentum of the system before and after the collision as a function of the relative speed v12 and the speed v1 of the particle created after the collision:
\[ \frac{m_{02}v_{12}}{\sqrt{1-\frac{v_{12}^{2}}{c^{2}}}}=\frac{m_{0}v_{1}}{\sqrt{1-\frac{v_1^{2}}{c^{2}}}} \]Relative velocity is the addition of velocities
The relative velocity v12 between the particles, measured by the observer O1, is the relativistic addition of their velocities.
To complete the proof, we set up an equation using the results of the two observers.
This gives the final expression for the relative velocity as a function of the velocities of the individual particles:
\[ v_{12} = \frac{v_1 + v_2}{1 + \frac{v_1v_2}{c^2}} \]This expression represents the relativistic addition of velocities.
The detailed version of this alternative proof of the relativistic addition of velocities is given in the tenth chapter of the book “Newton and Relativity“.
Another simpler proof applies to the relativistic addition of equal velocities.
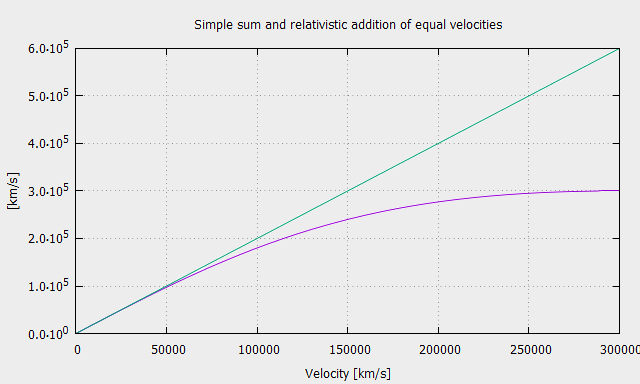
Use the Relativistic Calculator to calculate the relativistic addition of velocities.
Continue on the alternative path of relativistic proofs: Proof of the constancy of the speed of light.
______________
The aim of this website is to introduce the theory of relativity using a new, simple and accessible demonstration method.
To support this project, please order the book “Newton and Relativity“.



Leave a Reply