La derivazione della contrazione delle lunghezze può essere eseguita senza la trasformazione di Lorentz, usando la legge di conservazione dell’energia.
Questa derivazione rappresenta l’elemento finale nella sequenza di dimostrazioni relativistiche che ha preso l’avvio dal principio di equivalenza massa-energia ricavato dalla fisica classica.
Infatti dalla formula della contrazione delle lunghezze si ricavano facilmente le trasformazioni relativistiche per lo spazio e il tempo (vedi la dimostrazione).
Con quest’ultima derivazione raggiungiamo così anche lo scopo finale della trattazione presentata in questo sito web:
quello di dimostrare che la trasformazione di Lorentz – e di conseguenza la Teoria della Relatività Speciale – possa essere interpretata come il risultato di una logica estensione della Meccanica newtoniana.
Descrizione della dimostrazione in forma ridotta
(Per la versione dettagliata della dimostrazione rimandiamo all’undicesimo capitolo del libro “Newton e la Relatività”).
Per la derivazione della contrazione delle lunghezze immaginiamo in un esperimento ideale la collisione di un elettrone e un positrone.
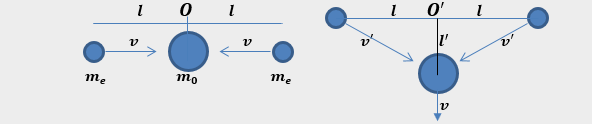
Si assume che in seguito all’urto si formi una nuova particella che si trovi nell’origine di un sistema di coordinate in quiete rispetto a un osservatore O.
Un secondo osservatore O’ si muove con la stessa velocità v dell’elettrone e del positrone, ma in direzione verticale.
Dal punto di vista di O, per la legge di conservazione dell’energia, è valida la seguente relazione:
\[ m_0c^2 = \frac{2m_{0e}c^2}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \quad (11.2)\]di bilancio energetico prima e dopo la collisione.
Dal punto di vista dell’osservatore O’, la particella formata dopo la collisione si muove verso il basso lungo l’asse verticale con la velocità v (vedi l’animazione).
Considerando che il tempo t che trascorre fino alla collisione sull’asse orizzontale è lo stesso per entrambi gli osservatori, dal teorema di Pitagora si ottiene:
\[ l^2+l’^2= v’^2t^2 \quad \quad (11.1)\]Applicando il principio di conservazione dell’energia dal punto di vista dell’osservatore O’, si ottiene la seguente relazione:
\[ \frac{m_0c^2}{\sqrt{1-\frac{v^2}{c^2}}} = \frac{2m_{0e}c^2}{\sqrt{1-\frac{v’^2}{c^2}}} \quad (11.3)\]Sostituendo a m0c2 il termine a destra della relazione (11.2), si ottiene:
\[ 1-\frac{v^2}{c^2} = \sqrt{1-\frac{v’^2}{c^2}}\]E tenendo conto della relazione (11.1), dopo semplici passaggi algebrici, si ricava la seguente relazione:
\[ l’=l\sqrt{1-\frac{v^2}{c^2}}\]che esprime la contrazione relativistica delle lunghezze in funzione della velocità.
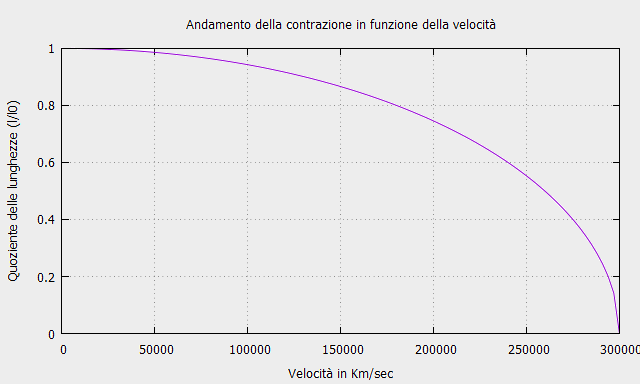
La versione dettagliata della derivazione della contrazione delle lunghezze è riportata nell’undicesimo capitolo del libro “Newton e la Relatività“.
______________
Con il Relativistic Calculator puoi calcolare la contrazione delle lunghezze in funzione della velocità.
Prosegui sul percorso alternativo delle dimostrazioni relativistiche: Trasformazione della coordinata spaziale e temporale.
Leave a Reply