Die Herleitung des relativistischen Dopplereffekts spielt eine Schlüsselrolle in der etablierten Ableitung der Relativitätstheorie.
Tatsächlich nutzte Einstein dieses aus den Gesetzen der Elektrodynamik abgeleitete Prinzip in seiner vierten Arbeit von 1905, um die Hypothese der Abhängigkeit der Trägheit eines Körpers von seinem Energieinhalt zu belegen.
Im folgenden Artikel wird gezeigt, wie der relativistische Doppler-Effekt auf einfache Weise nachgewiesen werden kann, indem die Grundsätze der Energie- und Impulserhaltung auf den physikalischen Prozess der Paarvernichtung angewendet werden.
Herleitung des Relativistischen Dopplereffekts in gekürzter Form
(Für die detaillierte Version der Herleitung verweisen wir auf das fünfzehnte Kapitel des Buches “Newton und die Relativität“).
Nach der Annihilation des Elektron-Positron-Paares entsteht ein instabiles Teilchen aus dessen Zerfall die Emission von zwei Photonen in entgegengesetzte Richtungen erfolgen kann:
Klicken Sie wiederholt auf die rechteckige Fläche, um den Vorgang anzuzeigen
Bei diesem Vorgang geht die gesamte Masse des Teilchens in die Energie 2hf der beiden emittierten Photonen über. Deswegen:
Für einen Beobachter in Ruhezustand
Für einen Beobachter, der sich in Ruhe mit dem Teilchen befindet, gilt die folgende Beziehung der Energieerhaltung vor und nach dem Teilchen-Zerfall:
\[ m_0c^2= 2hf \]Wobei:
m0 ist die Masse des nach der Annihilation gebildeten instabilen Teilchens
c ist die Lichtgeschwindigkeit im Vakuum
h ist das Plancksche Wirkungsquantum
f ist die zu den Photonen zugehörige elektromagnetische Frequenz
Für einen Beobachter in Bewegung
Für einen zweiten Beobachter, der sich stattdessen mit der Geschwindigkeit v bewegt, gelten die folgenden Beziehungen der Energie-:
\[ \frac{m_0c^2}{\sqrt{1-\frac{v^{2}}{c^{2}}}}=hf_1+hf_2\]und der Impulserhaltung:
\[ \frac{m_0v}{\sqrt{1-\frac{v^{2}}{c^{2}}}}=\frac{hf_1}{c}-\frac{hf_2}{c}\]vor und nach dem Zerfall des Teilchens.
Die Lösung der drei Gleichungen in Bezug auf die vom bewegten Beobachter gemessenen Frequenzen f1 und f2, als Funktion der vom ruhenden Beobachter festgestellten Frequenz f, führt zu den Beziehungen des relativistischen optischen Doppler-Effekts für eine sich nähernde Lichtquelle:
\[f_1=f\sqrt{\frac{c+v}{c-v}}\]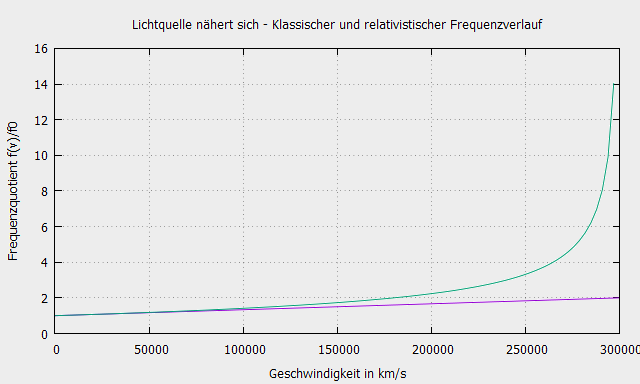
und für eine Lichtquelle, die sich entfernt:
\[f_2=f\sqrt{\frac{c-v}{c+v}}\]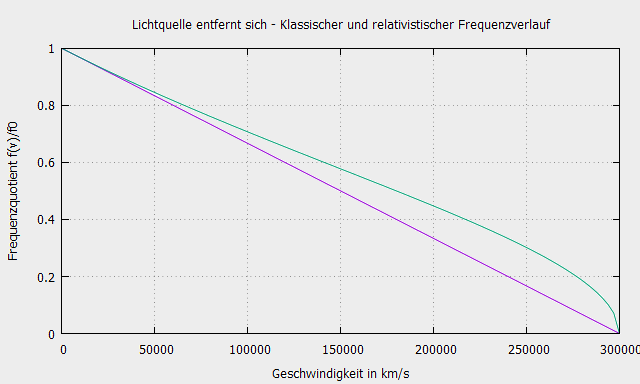
Auch für diesen Beweis, wie für alle anderen Beweise auf dieser Website, wird die Lorentz-Transformation nicht verwendet:
Tatsächlich werden nur die Prinzipien der Energie- und Impulserhaltung verwendet.
Die detaillierte Version der Herleitung des relativistischen Dopplereffekts wird im fünfzehnten Kapitel des Buches “Newton und die Relativität” beschrieben.
Mit dem Relativistic Calculator können Sie die Frequenzverschiebung in Abhängigkeit von der Geschwindigkeit berechnen.
Weiter auf dem alternativen Weg der relativistischen Beweise: Herleitung der relativistischen Beschleunigung.
______________
Das Ziel dieser Webseite ist es, die Relativitätstheorie mit einer neuen, einfachen und zugänglichen Demonstrationsmethode zu ergründen.
Um dieses Projekt zu unterstützen, bestellen Sie bitte das Buch “Newton und die Relativität“.



Leave a Reply