Eine alternative Herleitung der relativistischen Beschleunigung kann unter Verwendung des zweiten Gesetzes der Dynamik von Newton erfolgen.
(Dies ist eine gekürzte Fassung der Herleitung der relativistischen Beschleunigung. Für die detaillierte Version klicken Sie hier).
Ein einfacher Fall für den Nachweis der relativistischen Beschleunigung ist der einer Bewegung in die gleiche Richtung der einwirkenden Kraft. In diesem Fall reicht es aus, ein Verfahren zu verwenden, das auf einer Skalarberechnung basiert.
Nachweis mit Skalarberechnung
Der Nachweis der relativistischen Beschleunigung mit Skalarberechnung kann auf zwei Arten erfolgen:
- ausgehend von der impliziten Form F = d (mv)/dt des zweiten Gesetzes der Dynamik, indem m durch die relativistische Massenformel ersetzt wird (siehe Berechnungsverfahren).
- ausgehend von der expliziten Form F = mdv/dt + vdm/dt des zweiten Gesetzes der Dynamik, indem m durch die relativistische Massenformel und dm durch den äquivalenten Energieausdruck ersetzt wird (siehe Berechnungsverfahren).
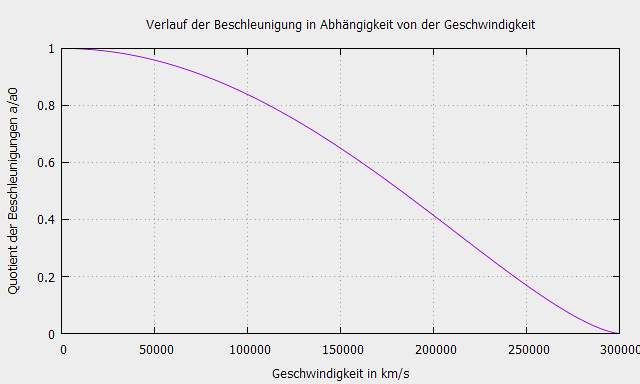
Im allgemeineren Fall, der auch Fällen vorsieht, in denen die Bewegungsrichtung von der Kraftrichtung abweicht, ist eine Herleitung auf der Grundlage einer Vektorberechnung erforderlich.
Als Ergebnis erhält man die longitudinale und die transversale Komponente der relativistischen Beschleunigung.
Nachweis mit Vektorberechnung
Der Beweis der relativistischen Beschleunigung mit der Vektorberechnung verwendet das Zweite Prinzip der Dynamik in allgemeinster Form.
Das Gesetz Newtons wird in diesem Fall durch die folgende Vektorbeziehung ausgedrückt:
\[ \vec{F}=\frac{d(m\vec{v})}{dt} \quad \Rightarrow \quad \vec{F}=\vec{v}\frac{dm}{dt}+m\frac{d\vec{v}}{dt}\quad\quad (16.1)\]Durch Einsetzen in Gleichung (16.1) der Beziehungen der Äquivalenz zwischen Energie und Masse:
\[ \frac{dm}{dt}=\frac{\vec{F}\circ\vec{v}}{c^2}\]und der relativistischen Masse:
\[ m = \frac{m_{0}}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \]erhält man die folgende Relation:
\[\vec{F}=\frac{\vec{F}\circ\vec{v}}{c^2}\vec{v}+\frac{m_{0}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}\frac{d\vec{v}}{dt}\quad\quad (16.8)\]Die Vektorberechnung führt zur Ableitung der longitudinalen und der transversalen Komponenten der relativistischen Beschleunigung:
\[ a_L=\frac{F_L}{m_0}\left(1-\frac{v^{2}}{c^{2}} \right)^\frac{3}{2} \quad ; \quad a_T=\frac{F_T}{m_0}\left(1-\frac{v^{2}}{c^{2}} \right)^\frac{1}{2} \]
Diese Herleitung zeigt, dass Newtons zweites Gesetz der Dynamik auch in Vektorform mit der Relativitätstheorie kompatibel ist.
Diese alternative Herleitung der relativistischen Beschleunigung wird in detaillierter Form im sechzehnten Kapitel des Buches “Newton und die Relativität” beschrieben.
______________
Mit dem Relativistic Calculator können Sie die relativistische Beschleunigung in Abhängigkeit von der Geschwindigkeit berechnen.
Leave a Reply