Eine alternative Herleitung der Längenkontraktion kann ohne Lorentz-Transformation unter Anwendung des Energieerhaltungssatzes erfolgen.
Diese Herleitung der Längenkontraktion stellt der letzte Schritt in der Reihe relativistischer Beweise dar, die mit dem aus der klassischen Physik abgeleiteten Prinzip der Masse-Energie-Äquivalenz begonnen hat.
Tatsächlich lassen sich die relativistischen Transformationen für Raum und Zeit leicht aus der Formel für die Längenkontraktion erhalten (siehe Beweis).
Mit dieser letzten Herleitung erreichen wir somit auch das Endziel der auf dieser Website präsentierten Diskussion:
die Aufgabe zu zeigen, dass die Lorentz-Transformation – und damit die Spezielle Relativitätstheorie – als Ergebnis einer logischen Erweiterung der Newtonschen Mechanik interpretiert werden kann.
Beschreibung der Herleitung der Längenkontraktion in reduzierter Form
(Für die detaillierte Version der Herleitung verweisen wir auf das elfte Kapitel des Buches “Newton und die Relativität“).
Zur Herleitung der Längenkontraktion stellen wir uns in einem Gedankenexperiment die Kollision eines Elektrons und eines Positrons vor.
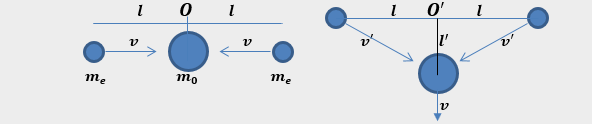
Es wird angenommen, dass sich infolge der Kollision ein neues Teilchen bildet, das im Ursprung eines zu dem Beobachter O ruhenden Koordinatensystems liegt.
Ein zweiter Beobachter O’ bewegt sich mit der gleichen Geschwindigkeit des Elektrons und des Positrons, jedoch in vertikaler Richtung.
Aus der Sicht von Beobachter O gilt wegen des Energieerhaltungssatzes vor und nach der Kollision folgende Beziehung des Energiebilanzen:
\[ m_0c^2 = \frac{2m_{0e}c^2}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \quad (11.2)\]Aus der Sicht des Beobachters O’ bewegt sich das nach der Kollision gebildete Teilchen mit der Geschwindigkeit v entlang der vertikalen Achse nach unten (siehe Animation).
Da die Zeit t, die bis zur Kollision auf der horizontalen Achse verstreicht, für beide Beobachter gleich ist, ergibt sich aus dem Lehrsatz des Pythagoras:
\[ l^2+l’^2= v’^2t^2 \quad \quad (11.1)\]Unter Berücksichtigung des Energieerhaltungssatzes ergibt sich aus der Sicht des Beobachters O’ folgende Beziehung:
\[ \frac{m_0c^2}{\sqrt{1-\frac{v^2}{c^2}}} = \frac{2m_{0e}c^2}{\sqrt{1-\frac{v’^2}{c^2}}} \quad (11.3)\]Durch Ersetzen von m0c2 durch den Term rechts von der Beziehung (11.2) erhalten wir:
\[ 1-\frac{v^2}{c^2} = \sqrt{1-\frac{v’^2}{c^2}}\]Und unter Berücksichtigung der Beziehung (11.1) wird nach einfachen algebraischen Schritten die folgende Relation erhalten:
\[ l’=l\sqrt{1-\frac{v^2}{c^2}}\]welche die relativistische Längenkontraktion in Abhängigkeit von der Geschwindigkeit ausdrückt.
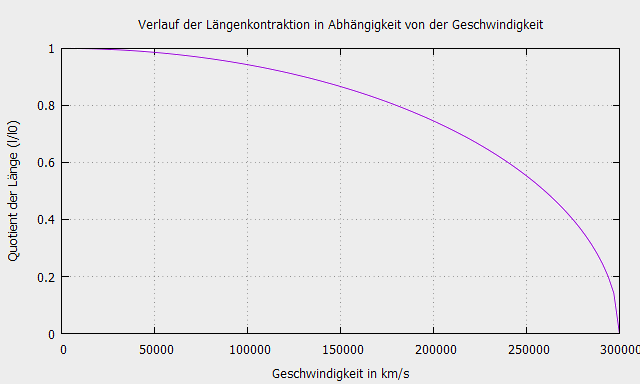
Wir möchten hiermit betonen, dass in dieser Abhandlung die relativistische Relation der Längenkontraktion hergeleitet wurde, ohne das Postulat der Konstanz der Lichtgeschwindigkeit voraussetzen zu müssen (siehe “Abfolge der relativistischen Herleitungen“).
Die detaillierte Fassung dieser Herleitung der Längenkontraktion und Zeitdilatation finden Sie im elften Kapitel des Buches “Newton und die Relativität“.
Mit dem Relativistic Calculator können Sie die Längenkontraktion in Abhängigkeit von der Geschwindigkeit berechnen.
Weiter auf dem alternativen Weg der relativistischen Beweise: Raumkoordinaten- und Zeit-Transformation.
______________
Das Ziel dieser Webseite ist es, die Relativitätstheorie mit einer neuen, einfachen und zugänglichen Demonstrationsmethode zu ergründen.
Um dieses Projekt zu unterstützen, bestellen Sie bitte das Buch “Newton und die Relativität“.



Leave a Reply