Derivation of the relativistic Doppler effect

The derivation of the relativistic Doppler effect plays a key role in the traditional derivation of the Theory of Relativity.

In fact, after deriving it from the laws of electrodynamics, Einstein used this principle in his fourth paper in the year 1905 to support the hypothesis of the dependence of the inertia of bodies on their energy content.

In the following article we will see how to demonstrate the relativistic Doppler effect in a simple way by applying the principles of conservation of energy and momentum to the physical process of pair annihilation.

Derivation of the Relativistic Doppler Effect in reduced form

(For the detailed version of the derivation we refer to the fifteenth chapter of the book “Newton and Relativity“).

After the annihilation of the electron-positron pair, an unstable particle is created.

The decay of this particle can then be followed by the emission of two photons in opposite directions:

Click repeatedly on the rectangular area to view the process

By this process, the entire mass of the particle is converted into the 2hf energy of the two photons emitted. Hence:

For an observer at rest

For an observer at rest with the particle, the following relationship of energy conservation applies before and after the particle decay:

\[ m_0c^2= 2hf \]

Where:

m₀ is the mass of the unstable particle created after annihilation

c is the speed of light in a vacuum

h is Planck’s Constant

f is the electromagnetic frequency of the photons

For an observer in motion

For a second observer who instead moves at the speed of v, the following energy relations:

\[ \frac{m_0c^2}{\sqrt{1-\frac{v^{2}}{c^{2}}}}=hf_1+hf_2\]

and momentum conservation apply:

\[ \frac{m_0v}{\sqrt{1-\frac{v^{2}}{c^{2}}}}=\frac{hf_1}{c}-\frac{hf_2}{c}\]

… before and after the particle decay.

Solving the three equations for the frequencies f1 and f2 measured by the moving observer as a function of the frequency f detected by the stationary observer gives the relativistic optical Doppler effect relations for an approaching light source:

\[f_1=f\sqrt{\frac{c+v}{c-v}}\]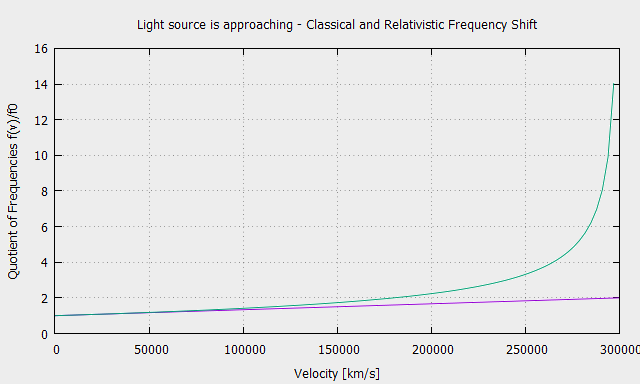

and for a receding light source:

\[f_2=f\sqrt{\frac{c-v}{c+v}}\]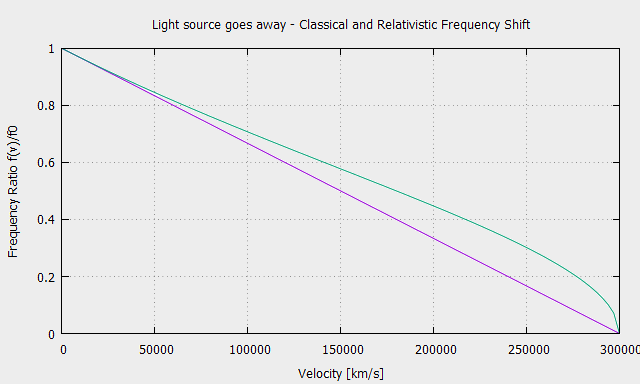

Again, as with all the other proofs on this site, we do not use the Lorentz transformation:

In fact, we use only the principles of conservation of energy and momentum.

You can find the detailed version of the derivation of the relativistic Doppler Effect in the fifteenth chapter of the book “Newton and Relativity“.

Use the Relativistic Calculator to calculate the Frequency Ratio as a function of speed.

Continue on the alternative path of relativistic proofs: Alternative derivation of relativistic acceleration.

Go to homepage

______________

The aim of this website is to introduce the theory of relativity using a new, simple and accessible demonstration method.

To support this project, please order the book “Newton and Relativity“.