An alternative derivation of relativistic acceleration can be performed using Newton‘s Second Law of Motion.
(This is an abridged version of the alternative derivation of relativistic acceleration. For the detailed version, click here).
A simple case of proof of relativistic acceleration is that of motion in the same direction as the force. In this case it is sufficient to use a procedure based on a scalar calculation.
Proof with scalar calculus
The proof of relativistic acceleration with scalar calculus can be done in two ways:
- Starting from the implicit form F = d (mv)/dt of the Second Law of Motion, by replacing m with the relativistic mass formula (see the calculation procedure).
- Starting from the explicit form F = mdv/dt + vdm/dt of the Second Law of Motion, by replacing m with the relativistic mass formula and dm with the equivalent expression of energy (see the calculation procedure).
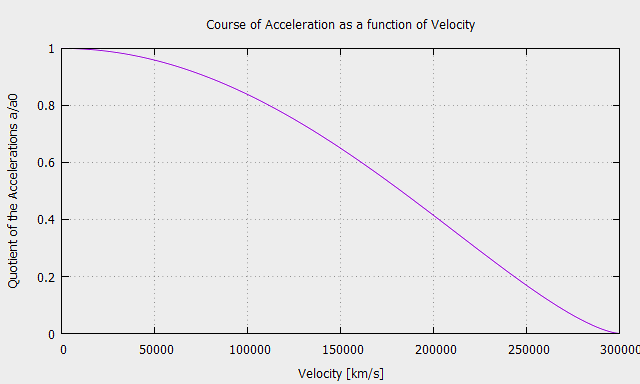
In the more general case, which also foresees situations in which the direction of motion is different from that of the force, it is necessary to perform a demonstration based on a vector calculation.
As a result, the longitudinal and transversal components of the relativistic acceleration are obtained.
Proof with vector calculus
The proof of relativistic acceleration with vector calculus uses the Second Law of Motion in its most general form.
In this case, Newton’s law is expressed by the following vector relationship:
\[ \vec{F}=\frac{d(m\vec{v})}{dt} \quad \Rightarrow \quad \vec{F}=\vec{v}\frac{dm}{dt}+m\frac{d\vec{v}}{dt}\quad\quad (16.1)\]Substituting into equation (16.1) the relations of equivalence between energy and mass:
\[ \frac{dm}{dt}=\frac{\vec{F}\circ\vec{v}}{c^2}\]and of relativistic mass:
\[ m = \frac{m_{0}}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \]one obtains the following relation:
\[\vec{F}=\frac{\vec{F}\circ\vec{v}}{c^2}\vec{v}+\frac{m_{0}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}\frac{d\vec{v}}{dt}\quad\quad (16.8)\]The vector calculation leads to the derivation of the longitudinal and transversal components of the relativistic acceleration:
\[ a_L=\frac{F_L}{m_0}\left(1-\frac{v^{2}}{c^{2}} \right)^\frac{3}{2} \quad ; \quad a_T=\frac{F_T}{m_0}\left(1-\frac{v^{2}}{c^{2}} \right)^\frac{1}{2} \]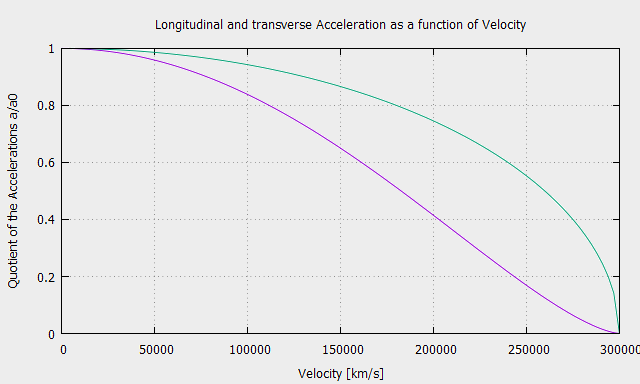
This alternative derivation shows that, also in vector form, Newton’s Second Law of Motion is compatible with the theory of relativity.
You find the detailed version of this alternative derivation of the relativistic acceleration in the sixteenth chapter of the book “Newton and Relativity”.
______________
With the Relativistic Calculator you can calculate the acceleration ratio a/a0 as a function of speed.
Leave a Reply