Dimostrazione Effetto Doppler relativistico

L’effetto Doppler relativistico gioca un ruolo chiave nella derivazione tradizionale della Teoria della Relatività.

Infatti Einstein – dopo averlo ricavato dalle leggi dell’elettrodinamica – si è servito di questo principio nel suo quarto lavoro dell’anno 1905 per avvalorare l’ipotesi della dipendenza dell’inerzia dei corpi dal loro contenuto energetico.

Col seguente articolo vedremo come una semplice dimostrazione dell’effetto Doppler relativistico possa essere fatta applicando i principi di conservazione dell’energia e della quantità di moto al processo fisico dell’annichilazione di coppia.

Dimostrazione dell’Effetto Doppler relativistico in forma ridotta

(Per la versione dettagliata della dimostrazione rimandiamo al quindicesimo capitolo del libro “Newton e la Relatività”).

In seguito all’annichilazione della coppia elettrone-positrone, si forma una particella instabile al cui decadimento può seguire l’emissione di due fotoni in direzioni opposte:

Cliccare ripetutamente la superficie rettangolare per farsi illustrare il processo

Con questo processo tutta la massa della particella si trasforma nell’energia 2hf dei due fotoni emessi. Perciò:

Per un osservatore in quiete

Per un osservatore che si trovi in quiete con la particella è applicabile la seguente relazione sulla conservazione dell’energia prima e dopo l’annichilazione:

\[ m_0c^2= 2hf \]

Dove:

m₀ è la massa della particella instabile formatasi dopo l’annichilazione

c è la velocità della luce nel vuoto

h è la costante di Planck

f è la frequenza elettromagnetica associata ai fotoni

Per un osservatore in moto

Per un secondo osservatore, che si muove con la velocità v nella direzione di uno dei due fotoni, sono invece valide le seguenti relazioni della conservazione dell’energia:

\[ \frac{m_0c^2}{\sqrt{1-\frac{v^{2}}{c^{2}}}}=hf_1+hf_2\]

e della quantità di moto, prima e dopo l’annichilazione:

\[ \frac{m_0v}{\sqrt{1-\frac{v^{2}}{c^{2}}}}=\frac{hf_1}{c}-\frac{hf_2}{c}\]

La risoluzione delle tre equazioni rispetto alle frequenze f₁ e f₂ misurate dall’osservatore in moto, in funzione della frequenza f rilevata dall’osservatore in quiete, conduce alle relazioni dell’Effetto Doppler ottico relativistico per una fonte luminosa che si avvicini:

\[f_1=f\sqrt{\frac{c+v}{c-v}}\]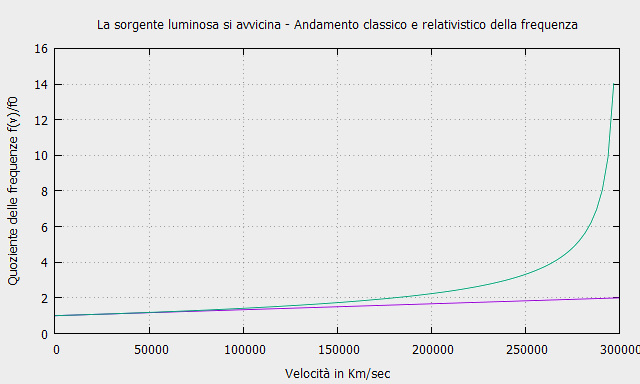

e per una fonte luminosa che si allontani:

\[f_2=f\sqrt{\frac{c-v}{c+v}}\]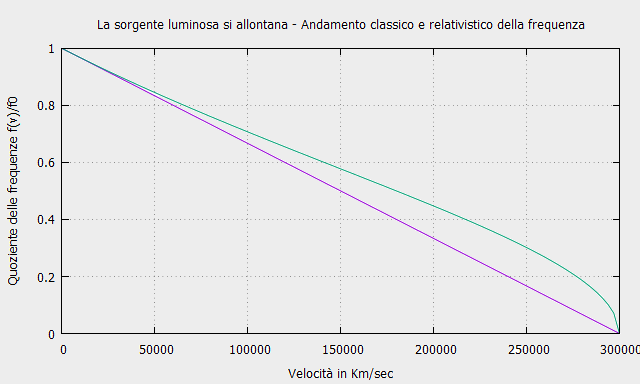

Anche per questa, come per tutte le altre dimostrazioni in questo sito, non viene usata la trasformazione di Lorentz:

Infatti, vengono utilizzati solo i principi di conservazione dell’energia e della quantità di moto.

La versione dettagliata della dimostrazione dell’Effetto Doppler relativistico è riportata nel capitolo quindicesimo del libro “Newton e la Relatività“.

______________

Con il Relativistic Calculator puoi calcolare la variazione di frequenza in funzione della velocità.

Prosegui sul percorso alternativo delle dimostrazioni relativistiche: dimostrazione dell’accelerazione relativistica.

Vai alla Home Page