Una derivazione dell’accelerazione relativistica può essere fatta utilizzando il Secondo Principio della Dinamica di Newton con la massa relativistica.
(Questa è una versione ridotta della derivazione dell’accelerazione relativistica. Per la versione dettagliata della dimostrazione rimandiamo al sedicesimo capitolo del libro “Newton e la Relatività”).
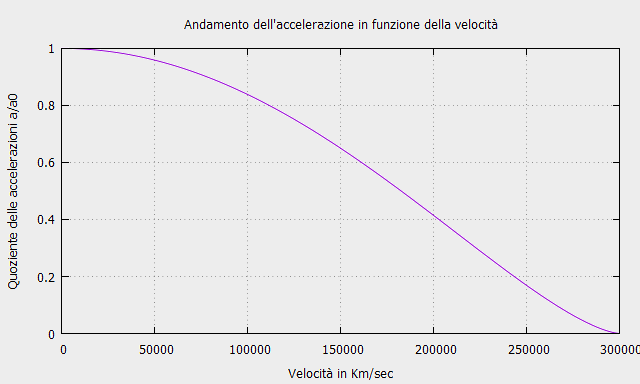
Un caso semplice di dimostrazione dell’accelerazione relativistica è quello di un moto nella stessa direzione della forza. In questo caso è sufficiente usare un procedimento basato su un calcolo scalare.
Dimostrazione col calcolo scalare
La dimostrazione dell’accelerazione relativistica col calcolo scalare può essere fatta in due modi:
- partendo dalla forma implicita F = d(mv)/dt del secondo principio della dinamica, per sostituzione di m con la formula della massa relativistica (vedi il procedimento di calcolo).
- partendo dalla forma esplicita F = mdv/dt + vdm/dt del secondo principio della dinamica, per sostituzione di m con la formula della massa relativistica e di dm con l’espressione equivalente dell’energia (vedi il procedimento di calcolo).
Nel caso più generale, che prevede anche situazioni in cui la direzione del moto è diversa da quella della forza, è necessario eseguire una dimostrazione basata su un calcolo vettoriale.
Come risultato si ottengono le componenti longitudinale e trasversale dell’accelerazione relativistica.
Dimostrazione col calcolo vettoriale
La dimostrazione dell’accelerazione relativistica col calcolo vettoriale utilizza il secondo principio della dinamica nella forma più generale.
La legge di Newton in questo caso viene espressa dalla seguente relazione vettoriale:
\[ \vec{F}=\frac{d(m\vec{v})}{dt} \quad \Rightarrow \quad \vec{F}=\vec{v}\frac{dm}{dt}+m\frac{d\vec{v}}{dt}\quad\quad (16.1)\]Sostituendo nella (16.1) le relazioni dell’equivalenza fra energia e massa:
\[ \frac{dm}{dt}=\frac{\vec{F}\circ\vec{v}}{c^2}\]e la formula della massa relativistica:
\[ m = \frac{m_{0}}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \]si ricava la seguente relazione:
\[\vec{F}=\frac{\vec{F}\circ\vec{v}}{c^2}\vec{v}+\frac{m_{0}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}\frac{d\vec{v}}{dt}\quad\quad (16.8)\]Eseguendo il calcolo vettoriale, si ottengono le seguenti componenti longitudinale e trasversale dell’accelerazione relativistica:
\[ a_L=\frac{F_L}{m_0}\left(1-\frac{v^{2}}{c^{2}} \right)^\frac{3}{2} \quad ; \quad a_T=\frac{F_T}{m_0}\left(1-\frac{v^{2}}{c^{2}} \right)^\frac{1}{2} \]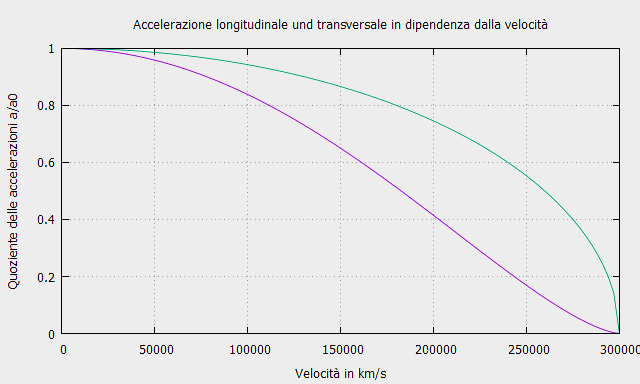
Questa dimostrazione mostra che anche in forma vettoriale il Secondo Principio della Dinamica di Newton è compatibile con la Teoria della Relatività.
La versione dettagliata della derivazione alternativa dell’accelerazione relativistica è riportata nel sedicesimo capitolo del libro “Newton e la Relatività“.
______________
Con il Relativistic Calculator puoi calcolare l’accelerazione relativistica in funzione della velocità.
Leave a Reply