An alternative derivation of the length contraction can be made without the Lorentz transformation, using the conservation of energy law .
This derivation is the final step in the sequence of relativistic demonstrations that started with the mass-energy equivalence principle derived from classical physics.
In fact, from the length contraction formula we can easily derive the relativistic transformations for space and time (see demonstration).
With this last derivation, we thus also reach the final purpose of the discussion presented on this website:
That is to show that the Lorentz transformation – and thus the Theory of Special Relativity – can be interpreted as the result of a logical extension of Newtonian mechanics.
Description of the proof in reduced form
(For the detailed version of the proof see chapter 11 of the book “Newton and Relativity“).
For the derivation of length contraction, we imagine in an thought experiment the collision of an electron and a positron.
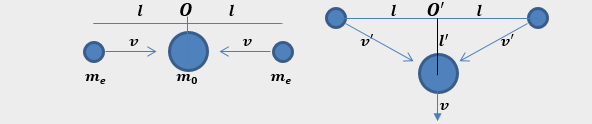
It is assumed that following the collision a new particle is created, which is at the origin of a coordinate system at rest with respect to an observer O.
A second observer O’ moves at the same speed as the electron and the positron, but in a vertical direction.
From the point of view of observer O:
According to the law of conservation of energy, the following energy balance relationship applies before and after the collision:
\[ m_0c^2 = \frac{2m_{0e}c^2}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \quad (11.2)\]From the point of view of observer O’:
The particle formed after the collision moves downwards along the Y axis at the speed v (see animation).
As the time t elapsed before the collision on the horizontal axis is the same for both observers, it follows:
\[ l^2+l’^2= v’^2t^2 \quad \quad (11.1)\]Considering the principle of energy conservation from the point of view of the observer O’, we obtain the following relationship:
\[ \frac{m_0c^2}{\sqrt{1-\frac{v^2}{c^2}}} = \frac{2m_{0e}c^2}{\sqrt{1-\frac{v’^2}{c^2}}} \quad (11.3)\]By replacing m0c2 with the term on the right of the relation (11.2), we obtain :
\[ 1-\frac{v^2}{c^2} = \sqrt{1-\frac{v’^2}{c^2}}\]And taking into account the relation (11.1), after some simple algebraic passages, we get the following relation, which expresses the relativistic contraction of lengths as a function of speed:
\[ l’=l\sqrt{1-\frac{v^2}{c^2}}\]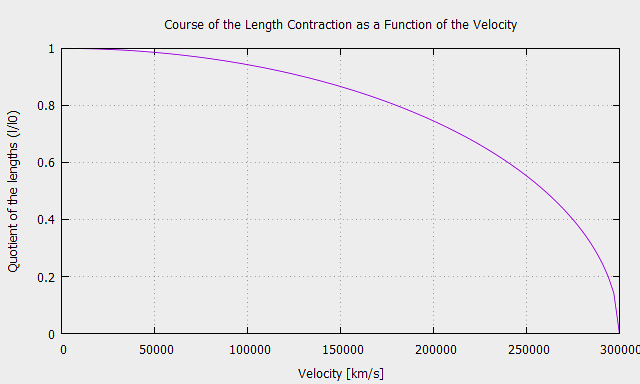
The detailed version of this alternative derivation of the length contraction and time dilation is given in the eleventh chapter of the book “Newton and Relativity“.
Use the Relativistic Calculator to calculate the length contraction as a function of speed.
Continue on the alternative path of relativistic proofs: Alternative derivation of the Lorentz transformations for space and time.
______________
The aim of this website is to introduce the theory of relativity using a new, simple and accessible demonstration method.
To support this project, please order the book “Newton and Relativity“.



Leave a Reply